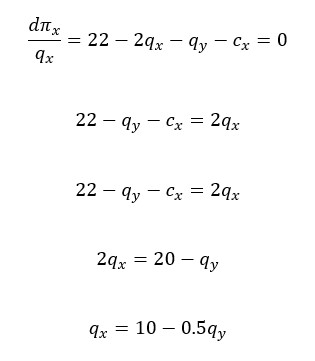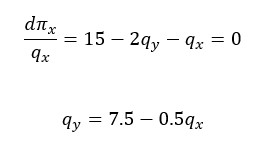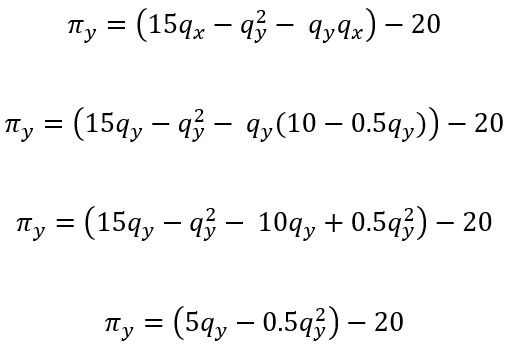Economics Problem Solving: Monopolistic and Cournot Competition

Part A

a.

Marginal cost(MC) =2

Market demand, p=22-q_x

Entry fee = $48

In the monopolistic market, the operating profit is total revenue (TR) – total cost (TC)

TR= p.Q = (22-qx). Q

TC = Fixed cost + variable cost

TC = (FC+MC.Q)

π = p. Q – (FC + MC. Q)

π = (p – MC) Q – FC

π = (22 – q_x – 2) q_x – 48

π = 20q_x – q_x² – 48

We use the derivative of the profit function with respect to q_x.

20 – 2q_x = 0

2q_x = 20

q_x = 10

Now we use the above value in the profit equation:

π = 20q_x – q_x² – 48

π = 20.10 – 10² – 48

π = 200 – 100 – 48

π = 52

Thus the optimal operating profit is $52

b.

considering that the entry fee is $48 which is lower than the operating profit at $52, X would enter the market.

PART-B

Cournot competition is where the companies compete on the amount of out they would produce.

MC of y = 7

Entry fee for y =20

Market demand, p = 22 – (q_x + q_y) = 22 – q_x – q_y

c.

for any given qy, the best response under Cournot competition would be to maximize their profit with respect to qx. Based on this the profit function would be:

π_x = (p – c_x) . q_x

π_x = (22 – q_x – q_y – c_x) . q_x

π_x = (22q_x – q_x² – q_y q_x – c_x q_x)

Now we take the derivative of the profit function with respect to q_x and set it equal to zero.

d.

the profit function of firm y would be the same as we have for x.

π_x = (22 – q_x – q_y – c_y) • q_y

We know marginal cost is provided as 7 using that in the equation:

π_x = (15 – q_x – q_y) • q_y

π_x = (15q_y – q_y² – q_y • q_x)

Using the first derivative and setting it to zero:

e.

To find equilibrium, we set q_x = q_y

10 – 0.5q_y = 7.5 – 0.5q_x

q_x = 5 + q_y

Now, we use the above value in either of the best response function.

We use,

Now, using the above value in q_x = 5 + q_y, q_x = 8.33 which is the equilibrium quantity for x

f.

p = 22 – q_x – q_y

p = 22 – 8.33 – 3.33 = $10.34

g.

For x, the profit function is:

π = (p – c_x) • q_x

We know the values, and we substitute them, which gives:

π_x = (10.34 – 2) • 8.33

π_x = 69.47

For y,

π_y = 11.122

Thus, for x, the operating profit is $69.47, and for y, it is $11.12

h.

we see that the entry fee is 48 for X while the profit is higher, so X will enter. For Y, though, the entry fee is 20, which is low, but it is higher than the operating profit, so Y will not enter.

i.

We see here that y won’t be entering, so this would be a monopoly, which means the market demand would be as highlighted in Part A, which is p=22-q_x

Here, we know the quantity which is 8.33, and when we substitute that

We have p = $13.67

Part C

j.

Y chooses whether to enter or not, and its capacity is qy.

X chooses second whether to enter or not, and the quantity chosen is qx.

Market demand remains same at : p =22 -(q_x+q_y) = 22- q_x – q_y

To identify the optimal point to enter, we need to calculate the profit-maximizing behavior of X, which means x is looking to choose q_x that would maximize its profit.

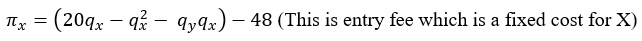
Using the first derivative, we get the same as before:

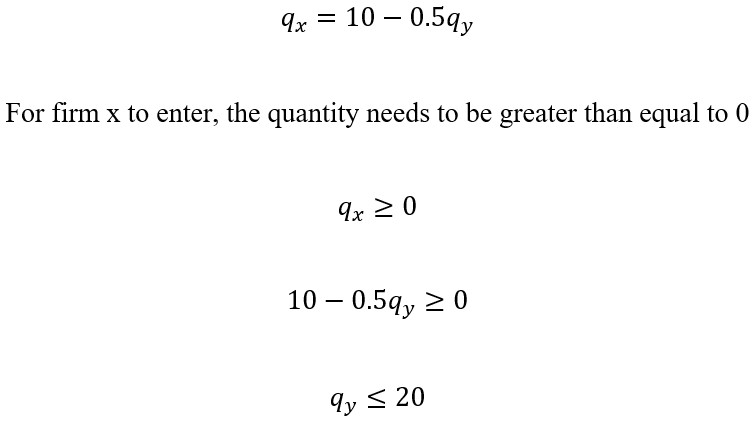
This means for firm X to enter the quantity of y, it needs to be less than or equal to 20.

k.

the best response for x is found to be
q_x=10-0.5q_y

We first look at the profit function for y, which is

Using the first derivative

5-q_y=0

q_y=5

The best response for y is qy=5

l.

The consumer surplus in monopoly would be lower when compared to Cournot. Cournot and sequential entry would benefit from the increased competition, but Corunot would not be as high as in perfect competition. Monopoly is low as it often charges a higher price, which reduces the area between the demand curve and price. In Cournot, it would reduce the price, and higher quantities would be available compared to monopoly.

Producer surplus would be higher in monopoly due to their ability to set the prices and capture the consumer surplus. In Cournot’s competition, the surplus would be shared, and each firm would have an incentive to produce more in order to gain more market share. In Sequential entry capacity competition, producer surplus would be lower than the other two due to capacity competition, leading to lower prices and quantities.

In total surplus which depends on specific equilibrium outcomes, the sequential entry and capacity competition would create a more competitive outcome, increasing the total surplus compared to Cournot. The surplus would be higher in Cournot’s competition since it is in imperfect competition. In monopoly, it’s the lowest due to deadweight loss linked with a higher price and a lower quantity.